محیط مستطیل | فرمول، مثال، راه حل

محیط مستطیل: یکی از کاربردی‌ترین علوم دنیا ریاضیات است. در علم ریاضی مفاهیم و اصول زیادی وجود دارد. یکی از اصلی‌ترین و اساسی‌ترین مباحث ریاضی، یافتن محیط اشکال هندسی است. به اندازه‌ی دور هر شکل هندسی محیط گفته می‌شود. به عبارت بهتر به میزان طول یک شکل هندسی در صورت قرار گرفتن در یک امتداد، محیط آن شکل اطلاق می‌شود. قبلا در برترآموز محیط مربع و محیط دایره و مساحت دایره را مورد بررسی قرار داده ایم، در این مقاله نیز به بررسی محیط مستطیل خواهیم پرداخت.

مستطیل یکی از اشکال مهم در ریاضیات و دنیای واقعی است. یافتن اندازه‌ی دور مستطیل، چه برای بلوک بندی زمین کشاورزی و چه برای بستن درز لای پنجره‌ها با نوار، همواره از اهمیت خاصی برخوردار است. این چهارضلعی که از دو جفت خط موازی ساخته می‌شود، فرمول خاصی برای محاسبه محیط دارد. چنانچه می‌خواهید فرمول محیط مستطیل را بدانید، کافی است که این مقاله را تا انتها بخوانید.

در ادامه این مقاله از برتر آموز قصد داریم تا با معرفی کامل مستطیل، و نحوه محاسبه‌ی فرمول آن، اندازه‌گیری محیط مستطیل با شکل را به شما آموزش دهیم. همچنین در پایان کار با ارائه‌ی مثال‌های مناسب شما را با اندازه‌گیری دور یک قطعه، جسم و زمین مستطیلی شکل آشنا خواهیم کرد. بنابراین این راهنما از سایت برتر آموز را از دست ندهید.

مستطیل چیست؟

مستطیل یک چهار ضلعی است که دارای دو جفت ضلع موازی ‌می‌باشد. هر جفت از ضلع‌های این شکل با هم برابر بوده و باید با هم موازی باشند. از سوی دیگر ضلع‌های متقاطع در محل تقاطع باید با هم زوایای 90 درجه تشکیل بدهند. بنابراین برای این که یک مستطیل رسم کنیم، باید 3 شرط مهم را رعایت کرده باشیم:

1. چهار ضلع ترسیم کنیم.
2. ضلع‌های روبرو با هم برابر و موازی باشند.
3. ضلع‌های مجاور با هم زاویه 90 درجه بسازند. (اضلاع مجاور باید قائمه باشند.)

پس یک شکل برای این که یک مستطیل باشد باید 3 شرط گفته شده را داشته باشد. در صورتی که یکی از موارد گفته شده نقض شود، شکل مورد نظر مستطیل نخواهد بود.

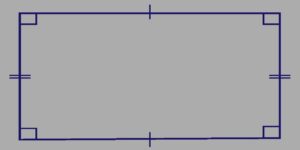
همانطور که در شکل بالا مشاهده می‌کنید، دو ضلع روبرو در مستطیل، علاوه بر موازی بودن، با هم برابرند. همچنین زوایای داخلی این شکل هندسی 90 درجه می‌باشند. در ادامه با محاسبه محیط مستطیل روش‌هایی برای اندازه‌گیری دور این شکل بدست خواهیم آورد.

تذکر: مستطیل یکی از انواع متوازی الاضلاع می‌باشد که زاویه‌های درونی آن 90 درجه است. به عبارت دیگر در صورتی که زاویه‌های داخلی یک شکل چهار ضلعی 90 درجه نباشد، ما با یک متوازی الاضلاع روبرو هستیم. همچنین اگر تمام اضلاع مستطیل با هم برابر باشند، چهارضلعی ما به یک مربع تبدیل خواهد شد.

اجزای مستطیل را بشناسیم

قبل از یافتن فرمول محیط مستطیل اجازه دهید، کمی بیشتر با این شکل هندسی آشنا شویم. تا به اینجا با نحوه‌ی ترسیم یک شکل مستطیلی آشنا شدید. همچنین اکنون می‌توانید با دیدن یک شکل به راحتی تشخیص دهید که یک چهار ضلعی مستطیلی است یا نه. حال زمان آن رسیده که با اجزای این شکل آشنا شویم.

در یک چهارضلعی مستطیلی شکل، ما باید 3 بخش مهم را بشناسیم:

• طول

بزرگترین ضلع همیشه طول نامیده می‌شود. فرقی نمی‌کند که این ضلع در چه راستایی باشد. معیار اصلی بزرگ‌تر بودن طول ضلع است. بنابراین بزرگترین ضلع را باید با طول نام‌گذاری کنیم. از آن جا که ما به دنبال یافتن محیط مستطیل با شکل هستیم، در این مقاله طول مستطیل را با a نمایش می‌دهیم.

• عرض

کوچکترین ضلع از لحاظ طول همیشه عرض اطلاق می‌شود. در اینجا نیز باید اشاره کنیم که فرقی نمی‌کند ضلع کوچک در چه راستایی قرار گرفته باشد. بنابراین کوچکترین ضلع این چهارضلعی را با عرض می‌شناسیم. برای راحتی کار عرض را نیز با b نمایش خواهیم داد.

• قطر

یکی دیگر از اجزای اصلی مستطیل قطر است. قطر اندازه‌ی وتری است که نقاط تقاطع این چهار ضلعی را به هم متصل می‌کند. هرچند در محاسبه محیط مستطیل قطر چندان کاربردی ندارد، اما یادگیری و فهم آن خالی از لطف نیست. قطر را نیز با d نامگذاری می‌کنیم.

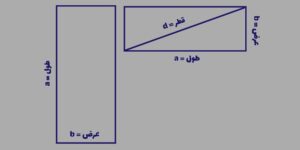
اکنون به طور کامل با چهارضلعی مهم ریاضیات آشنا شدید. حال تمام اجزای آن را نیز می‌شناسید. بنابراین در ادامه به سراغ محاسبه فرمول محیط مستطیل خواهیم رفت. پس اگر می‌خواهید طول دور یک شکل هندسی مستطیلی را با فرمول آن بدست آورید، فاصله‌ی زیادی با یادگیری نخواهید داشت.

فرمول محیط مستطیل با شکل

تا به اینجا مستطیل را شناختیم و با طول و عرض این شکل هندسی آشنا شدیم. در ادامه همانطور که قول دادیم، قصد داریم تا اندازه‌ی دور این شکل را به سادگی محاسبه کنیم. در واقع یافتن طول دور یک شکل مستطیلی کار چندان سختی نیست. در ادامه و برای راحتی کار محیط را با p نمایش خواهیم داد.

برای یافتن فرمول محیط مستطیل باید روند زیر را پیگیری کنیم:

چند مثال از محیط مستطیل

1. طبق تعریف محیط برابر است با اندازه دور یک شکل. مطابق با این تعریف ساده برای یافتن محیط یک شکل مستطیلی مانند شکل بالا، تمام اضلاع را با هم جمع می‌کنیم:

عرض + طول + عرض + طول = محیط

P = a + b + a + b

2. حال باید فرمول بالا را ساده سازی کنیم. در فرمول بدست آمده دو مقدار یکسان وجود دارد. بنابراین می‌توانیم این دو مقدار را با هم جمع ببندیم.

P = 2a + 2b

3. حال برای رسیدن به فرمول اصلی این شکل باید از عدد 2 فاکتور بگیریم. چنانچه می‌دانید چون عدد 2 ثابت است از بین دو عبارت خارج می‌شود و به صورت حاصل ضرب در مجموع دو ضلع نمایان می‌شود.

P = 2 (a+b)

طبق فرمول بدست آمده محیط یک شکل مستطیلی برابر است با دو برابر مجموع طول و عرض آن.

اکنون ما توانستیم به راحتی محیط مستطیل با شکل را محاسبه کنیم. بدیهی است که یک مستطیل دو جفت ضلع مساوی و برابر دارد. بنابراین با یافتن مجموع طول و عرض از این چهارضلعی، به راحتی می‌توان با دو برابر کردن عدد حاصل، مقدار محیط آن را محاسبه کرد.

نکته : از آن جا که محیط اندازه‌ی دور هر شکل، یا همان طول کلی شکل در امتداد یک خط را محاسبه می‌کند، بنابراین واحد آن بر حسب یکایی با توان یک خواهد بود. در واقع محیط یک مستطیل بسته به واحد طول و عرض آن، با واحدهایی مانند متر، سانتی‌متر، میلی‌متر، اینچ، یارد و غیره بیان می‌گردد.

چند مثال کاربردی

در ادامه پس از محاسبه‌ی فرمول این شکل هندسی می‌توانیم با ارائه چند مثال کاربردی بهتر با شیوه‌ی استفاده از این فرمول آشنا شویم. برای یادگیری و فهم بیشتر مبحث محیط مستطیل می‌توانید این چند مثال را تمرین کنید:

مثال 1 : طول و عرض یک مستطیل به ترتیب برابر 8 و 3.5 سانتی متر است. محیط این شکل چقدر خواهد بود؟

P = 2 ( 3.5 + 8 ) = 23

• با یک محاسبه‌ی ساده، محیط این شکل بدست می‌آید.

مثال 2 : اگر بخواهیم یک قطعه زمین کشاورزی مستطیلی به طول 1400 متر و عرض 300 متر را با بلوک‌های نیم متری حصار بکشیم، به چه تعداد از این بلوک‌های سیمانی بزرگ نیاز خواهیم داشت؟

• برای حل این سوال کافی است که اندازه‌ی دور زمین کشاورزی را محاسبه کنیم. همانطور که می‌دانید این مقدار با محیط مستطیل اندازه‌گیری می‌شود. همچنین برای محاسبه تعداد بلوک‌های موردنیاز باید طول دور زمین (محیط) را بر طول هر بلوک تقسیم کنیم.

P = 2 ( 1400 + 300 ) = 3400

N = 3400 / 0.5 = 6800

• بنابراین باید برای کشیدن حصار دور این زمین کشاورزی باید از 6800 بلوک استفاده کنیم.

مثال 3 : محیط یک قاب شیشه‌ای مستطیلی 25 سانتی متر است. اگر طول ضلع بزرگتر این قاب 7.5 سانتی متر باشد، طول ضلع کوچکتر را بیابید.

• در این مسئله برخلاف دو مسئله قبلی باید با استفاده از فرمول محیط مستطیل ، عرض آن را پیدا کنیم. این کار به سادگی با استفاده از فرمولی که در این مقاله بدست آوردیم میسر خواهد بود.

P = 2 ( 7.5 + b ) = 25

7.5 + b = 12.5

B= 5

• بنابراین طول عرض این مستطیل معادل 5 سانتی متر بوده است.

جمع بندی

مستطیل یکی از اشکال پرکاربرد در ریاضیات است و ارتباط تنگاتنگی با دنیای روزمره ما دارد. ما روزانه با تعداد زیادی از اجسام مواجه می‌شویم که شکلی مانند مستطیل دارند و به همین جهت فرا گرفتن محیط و مساحت این شکل هندسی می‌تواند بسیار حائز اهمیت باشد.

در این مقاله سعی کردیم تا با ارائه مطالبی کامل از این شکل هندسی، آن را به شما معرفی کنیم. همچنین طول، عرض و قطر این شکل نیز به طور کامل برای شما تعریف شد. اکنون به راحتی می‌توانید یک مستطیل دقیق رسم کنید و یا اشکال مستطیلی را تشخیص دهید. همچنین سه شرط مهم برای مستطیلی بودن یک شکل نیز بیان شد. اگر این سه شرط را به خوبی مطالعه نکردید، پیشنهاد می‌کنیم بازگردید و یک بار دیگر این سه شرط مهم را دوباره بخوانید.

اگر سوالی پیرامون این مبحث دارید، می‌توانید آن را با ما در میان بگذارید تا به شما کمک کنیم.