


مساحت دایره به زبان ساده | به همراه مثال های حل شده
مساحت دایره به زبان ساده: مساحت دایره یکی از ساده ترین فرمول های مساحت را دارد؛ تمام آنچه برای محاسبه آن نیاز داریم شعاع دایره است. اما همیشه مسئله به همین سادگی نیست! گاهی اوقات اطالاعاتی که مسئله در اختیار ما می گذارد اطلاعات پیچیده تری هستند به هر حال در این مقاله از برتر آموز باهم تمام روش های مختلف محاسبه مساحت دایره را در شرایطی که مساله به شما شعاع، قطر، محیط دایره و یا مساحت قطاعی از دایره را داده باشد در این پست برتر آموز بررسی خواهیم کرد. در این پست میتوانید محیط دایره را بدانید چقدر است.
اگر شعاع را دارید و خیلی سریع می خواهید به مساحت دایره برسید و وقتی برای انجام محاسبات ندارید می توانید مقدار شعاع را در بخش enter value این لینک وارد کنید تا مساحت دایره مورد نظرتان را برای شما محاسبه کند.
پیش از شروع فرمول مساحت دایره را می توانید در تصویر زیر ببینید.
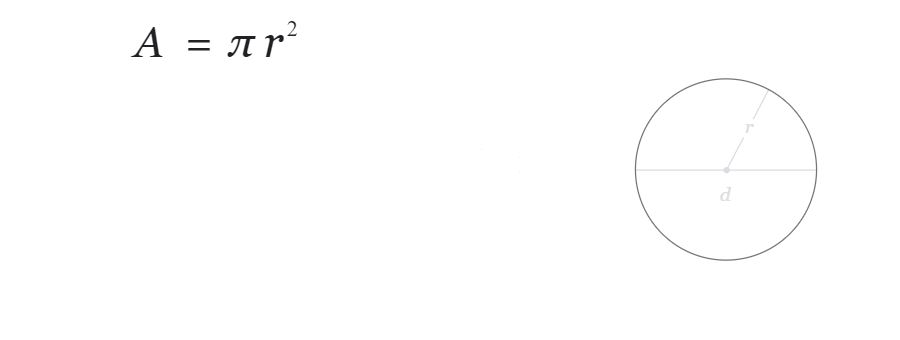
r که از کلمه radius گرفته شده است شعاع دایره و Diameter که دو برابر شعاع است قطر دایره (d) می باشد.
بخشی از مفاهیم پایه مربوط به دایره:
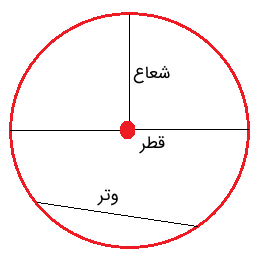
تعریف شعاع دایره: طول یک پاره خط از مرکز دایره تا نقطه ای روی محیط دایره است. شعاع در تمامی قسمت های دایره مقداری ثابت است.
تعریف قطر دایره: قطر بزرگ ترین وتر دایره است. وتر پاره خطی است که دو نقطه روی محیط دایره را به هم وصل می کند. در واقع، می توان چنین گفت که قطر پاره خطی است که دو نقطه دایره را به هم وصل می کند و از مرکز دایره نیز عبور می کند. قطر نیز مقدار ثابتی دارد.
تعریف قطاع دایره: قطاع یک دایره بخشی است که نام دیگر آن «گُوِه» می باشد. یک قطاع با کشیدن دو شعاع از مرکز به لبه دایره تعریف شده و فضای بین این دو شعاع را قطاع می نامند. (شکل آن را در بخش “محاسبه مساحت دایره با در اختیار داشتن یک قطاع از دایره” می توانید مشاهده کنید.)
عدد پی: در فرمول مساحت دایره یک المان دیگر به غیر از شعاع دایره نیز مشاهده می کنید، نام این علامت، پی است؛ عدد پی که به نام ثابت ارشمیدس نیز از آن یاد می شود عددی حقیقی و گُنگ است که با توجه به قوانین هندسه اقلیدسی از محاسبه نسبت محیط دایره به قطر آن بدست می آید و کاربردهای فراوانی در ریاضیات، فیزیک و مهندسی دارد. (اگر می خواهید برای آشنایی بیشتر با علم فیزیک می توانید مقاله ی آموزش فیزیک را مطالعه کنید.)
این عدد را در مسائل ساده معمولا برابر با 3.14 یا 3 در نظر می گیریم. در حالی که پی یک عدد با اعشار بی نهایت است.
عدد پی با 15 رقم اعشار :
π= 3.14159265359
پیش از شروع آموزش انواع روش های محاسبه مساحت دایره به این نکته توجه داشته باشید که تمام مساحت هایی که به دست آورده می شود تقریبی هستند چرا که همانطور که گفتیم عدد pi عددی گنگ است و مقدار دقیقی برای آن وجود ندارد؛ ما در مسائل زیر pi را 3.14 در نظر می گیریم.
مساحت دایره به زبان ساده: محاسبه مساحت دایره با در اختیار داشتن شعاع یا قطر
ساده ترین حالت محاسبه مساحت دایره آن است که مسئله شعاع یا قطر دایره را در اختیار شما قرار داده باشد؛ به مثال زیر توجه کنید:
مساحت دایره ای را محاسبه کنید که شعاع آن برابر با 6 سانتی متر است.
مرحله 1: شعاع داده شده را به توان دو برسانید :
مرحله 2: با توجه به فرمول A= Pi*r^2 اکنون باید حاصل بدست آمده را در عدد پی ضرب کنیم؛ یعنی:
- A=3.14 * 36 = 113.04
اکنون فرض کنید که مساله به صورت زیر مطرح شده باشد:
مساحت دایره ای را محاسبه کنید که قطر آن برابر با 12 سانتی متر است.
این مساله در واقع همان مساله قبلی است! حل کردن تنها یک مرحله بیشتر دارد.
مرحله 1: همانطور که گفتیم قطر دو برابر شعاع است؛ بنابرین برای به دست آوردن شعاع کافیست قطر را تقسیم بر دو کنید. به این صورت:
- d/2 = 12/2 = 6
مرحله 2: شعاع به دست آورده را به توان دو برسانید:
مرحله 3: با توجه به فرمول A= Pi*r^2 اکنون باید حاصل بدست آمده را در عدد پی ضرب کنیم؛ یعنی:
- A=3.14 * 36 = 113.04
به همین سادگی مساله حل شد! اما رایج ترین خطا در هنگام استفاده از قطر برای محاسبه مساحت دایره، به توان دو رساندن قطر و سپس تقسیم آن بر دو است. پس دقت کنید که حتماً ابتدا قطر را تقسیم بر دو کنید، سپس آن را به توان دو برسانید، در غیر این صورت جواب اشتباه خواهد بود.
پیشنهاد ویژه : اگر به فکر افزایش درآمد خود هستید و می خواهید با یک کار پاره وقت، بتوانید کسب درآمد مناسبی برای خودتان داشته باشید، توصیه می کنیم از صفحه آموزش تولید محتوا دیدن فرمایید.
مساحت دایره به زبان ساده: محاسبه مساحت دایره با در اختیار داشتن محیط دایره
پیش از شروع به فرمول محیط دایره که در تصویر زیر نشان داده شده است توجه کنید:
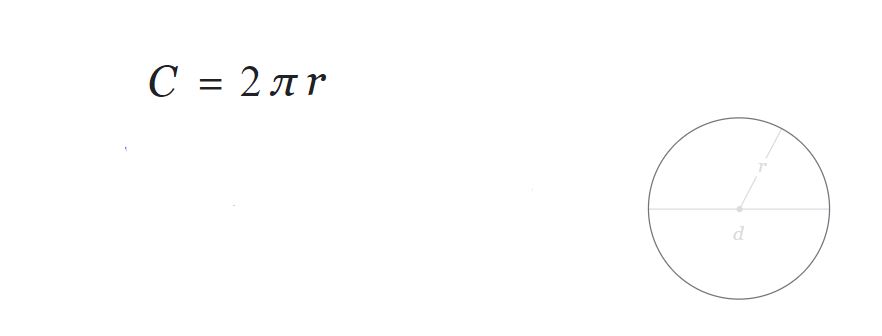
همانطور که می بینید در فرمول محیط دایره نیز تنها از شعاع دایره استفاده شده است. در تصویر بالا مجیط را با C نمایش داده است اما ما در ادامه برای حل مسائل محیط را طبق قرار داد معمول با P نمایش خواهیم داد.
اکنون به مثال زیر توجه کنید:
مساحت دایره ای با محیطی به طول 20 سانتی متر را محاسبه کنید.
برای حل کردن این مساله مراحل زیر را طی می کنیم:
مرحله 1: با توجه به فرمول محیط برای بدست آوردن شعاع دایره باید محیط داده شده را تقسیم بر 2pi کنیم؛ برای آسان تر شدن ادامه محاسبات تا مرحله آخر عدد pi را در مساله جایگذاری نمکنیم؛ به این صورت:
- P / 2pi =20 / 2pi = 10 / pi
مرحله 2: شعاع به دست آورده را به توان دو برسانید:
مرحله 3: با توجه به فرمول A= Pi * r^2 اکنون باید حاصل بدست آمده را در عدد پی ضرب کنیم؛ یعنی:
- A= pi * (100 / pi^2) = 100/pi
- A= 100 / pi= 31.84
برای آنکه این محاسبات آسان تر شود می توانید از یک فرمول استفاده کنید تا بدون نیاز به طی کردن 3 مرحله در یک مرحله و به صورت مستقیم به مساحت برسید.
فرمول محاسبه مساحت دایره با استفاده از محیط دایره: A= P^2 / 4pi
مساله بالا را با استفاده از این فرمول به این صورت حل می کنیم:
مرحله 1: محیطی که مساله داده است را به توان دو می رسانیم؛ به این صورت:
- P^2= 20^2= 400
مرحله 2: عدد به دست آمده را در فرمول A= P^2/ 4pi میگذاریم:
- A= 400 / 4pi = 100 / pi
مرحله 3: عدد pi را جایگذاری میکنیم تا جواب عددی را بدست بیاوریم.
- A= 100 / pi= 31.84
مساحت دایره به زبان ساده: محاسبه مساحت دایره با در اختیار داشتن یک قطاع از دایره
محاسبه مساحت دایره با در اختیار داشت مساحت یک قطاع از دایره تقریبا به سادگی مدل های قبلی محاسبه مساحت نیست. به مثال زیر توجه کنید:
قطاعی با زاویه مرکز 45 درجه از دایره O مساحتی برابر با 15pi دارد، مساحت کل دایره را بیابید. با توجه به زاویه ای که مرکز قطاع دارد به عبارتی دیگر می تواند گفت ما یک هشتم از مساحت کل دایره را داریم و مساحت کل دایره را می خواهیم؛ در این حالت راه حل بسیار ساده است پاسخ ما 15pi * 8 یعنی 120pi خواهد بود. اما به هر حال برای آن که بدانید این اعداد دقیقا از کجا به دست می آید و برای آن که بتوانید مساحت دایره با هر زاویه ای که به شما داده می شود را بدست بیاورید به راه حل های زیر توجه کنید:
برای محاسبه مساحت دایره با شرایط بالا ابتدا باید فرمول مساحت قطاع دایره را بدانیم:
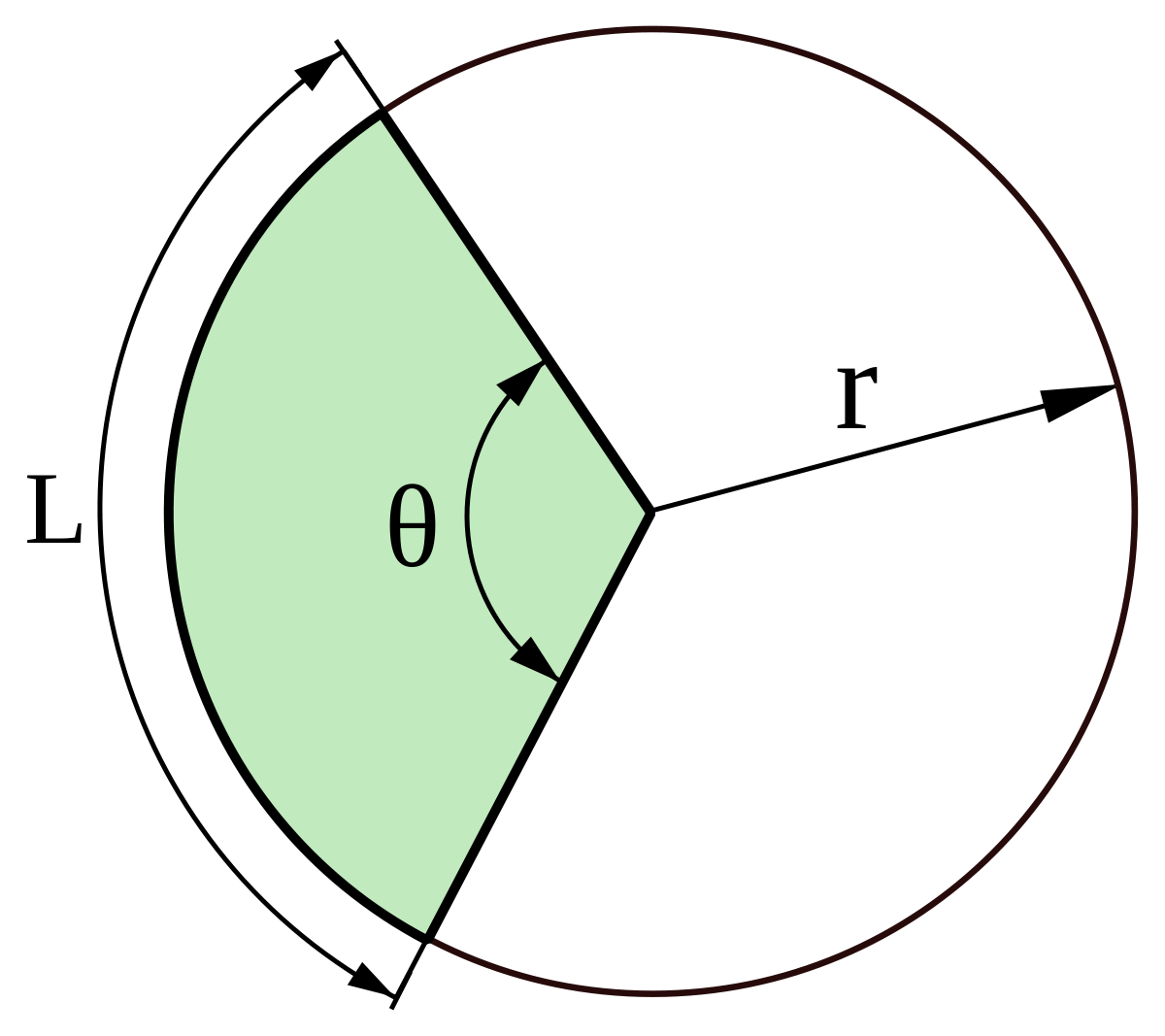

مرحله 1: با توجه به اینکه مساله زاویه را بر حسب درجه به ما داده است، با استفاده از فرمول دومی که در تصویر می بینید مساله را حل می کنیم. اگر اطلاعات دیگر و زاویه قطاع را که مساله در اختیار ما گذاشته است در فرمول منتخب بگذاریم معادله زیر بدست می آید:
- A= 15pi= (45pi * r^2) / 360
مرحله 2: بعد از ساده کردن عبارت بالا، معادله به شکل زیر در می آید؛ اکنون می توانیم معادله را حل کنیم.
- 1= (3/360) * r^2
- r^2= 120
مرحله 3: اکنون که r^2 را بدست آورده ایم می توانیم آن را در فرمول مساحت دایره بگذاریم:
- A= pi * r^2= pi * 120
- محاسبه میکنیم: A= 376.8
برای محاسبه مساحت دایره با شرایط بالا می توانیم از فرمول اصلاح شده ی زیر نیز استفاده کنیم:
فرمول به دست آوردن مساحت دایره با استفاده از مساحت یک قطاع از دایره:
مساحت دایره = مساحت قطاع * ( 360 / زاویه مرکز قطاع بر حسب درجه )
مراحل حل مساله بالا با استفاده از فرمول ساده شده به شرح زیر است:
مرحله 1: مقادیر معلوم را در فرمول قرار می دهیم. ( Ac مساحت دایره، As مساحت قطاع دایره و c زاویه مرکزی قطاع است (همان تتا). )
- Ac= As * (360 / c )
- Ac= 15pi * ( 360 / 45 )
مرحله 2: مساحت را بدست می آوریم:
- Ac= 120pi
- Ac= 376.8
مساحت دایره چیست؟
شکل هندسی دایره جزو یکی از پرکاربرترین اشکال هندسی در ریاشیات است که خوب طبیعتا شما باید مساحت و محیط آن را به خوبی باد باشید.
برای محاسبه مساحت دایره شما به فورمول مساحت دایره نیاز دارید که خوب در ادامه این مورد را بررسی خواهیم کرد:
زمانی که اندازه سطح یک دایره را بدست میآوریم مساحت آن را محاسبه کردهایم.
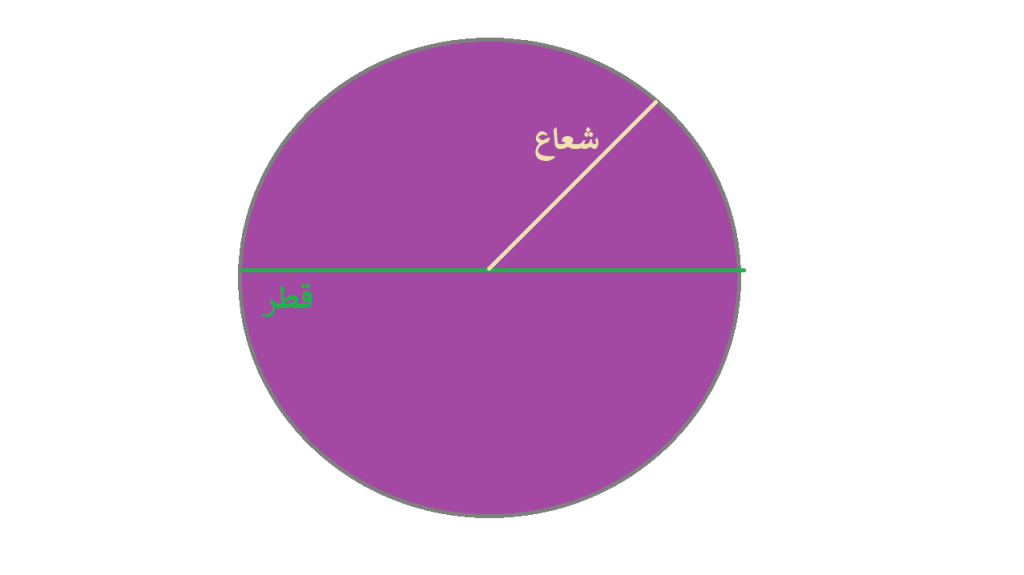
برای مثال در تصویر بالا ما به قسمت بنفش رنگ مساحت دایره میگوییم و همانطور که در این آموزش به شما توضیح دادیم برا فرمول مساحت دایره به چند پارامتر نیازداریم.
شعاع
قطر
عددی پی
روش محاسبه مساحت دایره چگونه است؟
فرمول مساحت دایره به صورت جبری به شرح زیر است :
شعاع × شعاع × عدد پی = مساحت دایره
شعاع × شعاع × 14/3= مساحت دایره
طبق دانستهها عدد پی همان 3.14 است و شعاع در مسئله به شما داده میشود و تنها با یک ضرب ساده میتوانید مساحت دایره را با فرمول بالا بدست آورید.
در اکثر کتب ریاضی ممکن است مساحت دایره فرمول را به شیوه زیر ببینید و این بازنویسی شده همان فرمول مساحت به زبان ریاضی به صورت بالا است :
S=π×r×r
فرمول مساحت دایره بر حسب قطر چگونه است ؟
خوب تا به الان ما تمامی مساحتهای دایره را بر حسب شعاع حساب کردیم حالا اگر در مسئله به ما قطر دادند باید چگونه مساحت را حساب کنیم؟
میدانیم که اندازه قطر، دو برابر اندازه شعاع است. حالا نسبت قطر و شعاع دایره را میتوان به صورت زیر محاسبه کرد:
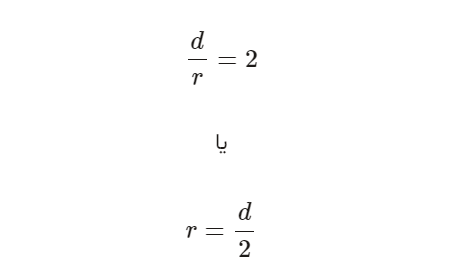
خوب حالا خیلی راحت عدد شعاع یا همان r را طبق فرمول بالا بدست بیاورید و سپس داخل فورمول مساحت دایره جایگذاری نمایید.
اگر میخواهید راجب به فرمول محیط دایره اطلاعات خوبی بدست بیارید حتما مقاله محیط دایره را مطالعه نمایید.
رابطه بین مساحت دایره و محیط دایره چیست؟
فرمول مساحت دایره را میتوان بر حسب محیط دایره بدست آوریم. بر اساس اندازه محیط و شعاع ، مساحت دایره برابر است با:
شعاع × نصف محیط دایره = مساحت دایره
آیا حفظ کردن فرمول مساحت دایره آسان است؟
معمولا دانش آموزان برای حفظ کردن فرمولهای مساحت و محیط کمی مشکل دارند اما در مورد دایره اگر شما با تمرین و تکرار به حل مسائل مختلف بپردازید متوجه خواهید شد که به خوبی این فرمول را یاد گرفتهاید و اصلا نیازی به حفظ کردن نیست!
پیشنهاد میشود مسائل مربوط به مساحت و محیط دایره را در کتاب درسی خود به خوبی حل نمایید. اگر سوالی درمورد فرمول مساحت دایره دارید لطفا در قسمت کامنت با دوستان برترآموزی به اشتراک بگذارید.

نظرات کاربران