روش حساب کردن مساحت مثلت ✔️ فرمول و مثال

مساحت مثلث: پیش تر در برتر آموز در مورد مساحت مربع و مساحت دایره صحبت کرده بودیم، امروز نیز میخواهیم شکل هندسی مثلث، انواع آن و مساحت حالت های مختلف آن را مورد بررسی قرار دهیم. و از آنجایی که مثلث از اشکال بسیار پرکاربرد و پایه در علوم ریاضی و هندسه است، یادگیری درست و مفهومی آن جز ملزومات است، به همین دلیل در این مقاله سعی کردیم تا مبحث مساحت مثلث را تا حد ممکن کامل و با جزئیات توضیح دهیم؛ با ما همراه باشید.

آشنایی با مثلث 

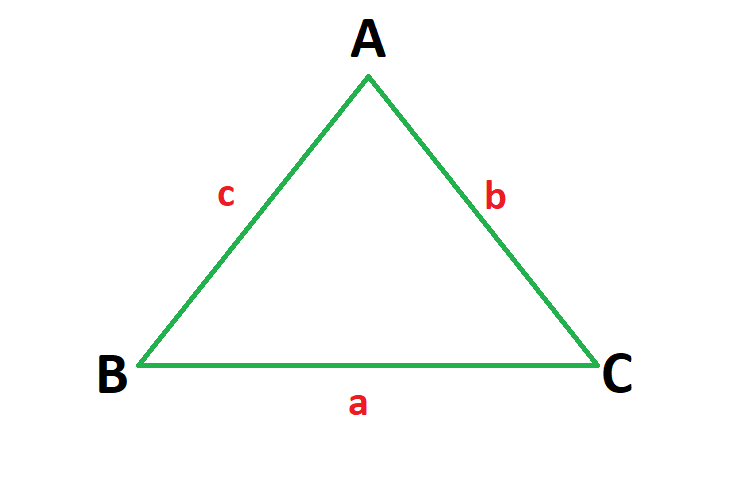
از جمله اشکال هندسی پایه و پُرکاربرد در مسائل مختلف ریاضی، هندسه و مهندسی، می‌توان به مثلث‌ ها اشاره کرد. مثلث یا سه‌ گوش، یک چند ضلعی مسطح با سه ضلع است که از اتصال سه خط غیر هم راستا در یک صفحه و در سه نقطه­ی متمایز به وجود می‌آید. به طورکلی، اجزای هر مثلث شامل سه ضلع، سه زاویه و سه ارتفاع است. در شکل زیر شمای کلی یک مثلث با اجزای آن به طور کامل نشان داده شده است. دو پارامتر مهم در مورد این شکل محیط و مساحت مثلث است.

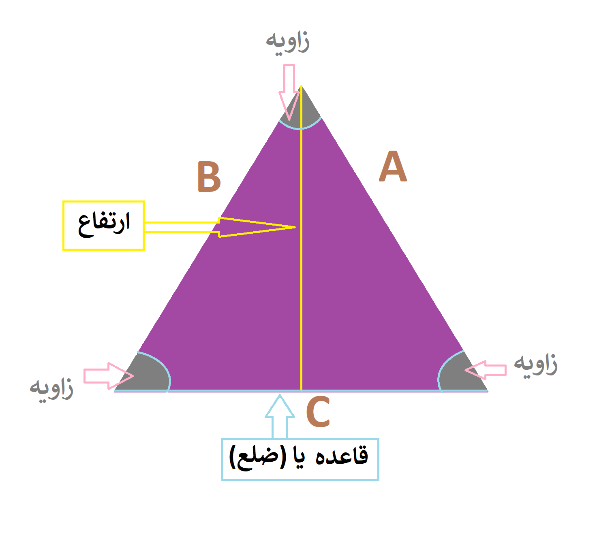
شکل 1. شکل و اجزای کلی یک مثلث. A,B,C همان قاعده یا اضلاع مثلث هستند.

با توجه به شکل 1 ویژگی‌های یک مثلث در حالت کلی شامل موارد زیر است:

• هر مثلث ممکن است دو یا سه ضلع هم‌اندازه داشته باشد یا اینکه هیچ ضلع برابری نداشته باشد.
• هر مثلث ممکن است دو یا سه زاویه­ی برابر داشته باشد یا اینکه هیچ زاویه­ی برابری نداشته باشد.
• هر مثلث دارای ۳ ارتفاع است که به عنوان پاره‌خطی از راس مثلث به ضلع مقابل آن عمود می‌شوند (در شکل 1 یکی از ارتفاع­ ها نشان داده شده است).
• مجموع زاویه‌های داخلی مثلث، برابر ۱۸۰ درجه است.
• مجموع زوایای خارجی در هر مثلث، برابر ۳۶۰ درجه است.
• اندازه­ی یک زاویه­ی خارجی در یک مثلث، برابر با مجموع دو زاویه داخلی غیر­مجاور آن است.
• هر مثلث دارای ۳ نیم­ساز داخلی و ۳ نیم­ساز خارجی است که از هر راس مثلث می­گذرد و آن را به دو زاویه­ی مساوی تقسیم می‌کنند.

نکته­: توجه داشته باشید که از هر ضلعی می‌توان به عنوان قاعده­ استفاده کرد، فقط باید مطمئن باشید که ارتفاع مثلث را از زاویه‌ ای در نظر بگیرید که به قاعده عمود است.

بر این اساس، انواع مختلفی از مثلث ­ها می­تواند وجود داشته باشد که در ادامه با آن ها آشنا خواهید شد.

انواع مثلث بر اساس اندازه ­ی اضلاع:

مثلث‌ها بر اساس اندازه ی اضلاع (یا اندازه زوایای داخلی) به سه دسته تقسیم می‌شوند:

• مثلث متساوی‌الاضلاع
• متساوی‌الساقین
• اسکالن

در جدول 1 می­ توانید انواع این مثلث­ ها را به همراه شکل و ویژگی­ های آن (اندازه ­ی اضلاع و اندازه­ ی زوایا) ملاحظه کنید.

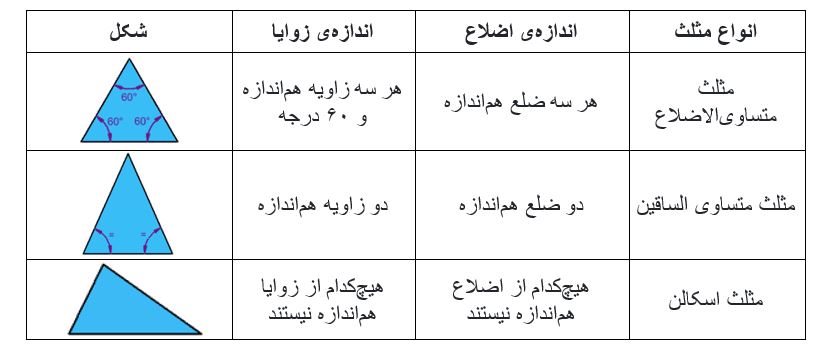
جدول 1

انواع مثلث بر اساس اندازه ­ی زاویه:

مثلث‌ ها براساس زوایا نیز دارای نام‌ گذاری‌های متفاوتی هستند. در جدول 2 انواع مثلث­ ها بر اساس اندازه­ ی زاویه ­ی داخلی آن ها به همراه شکلشان گردآوری شده است.

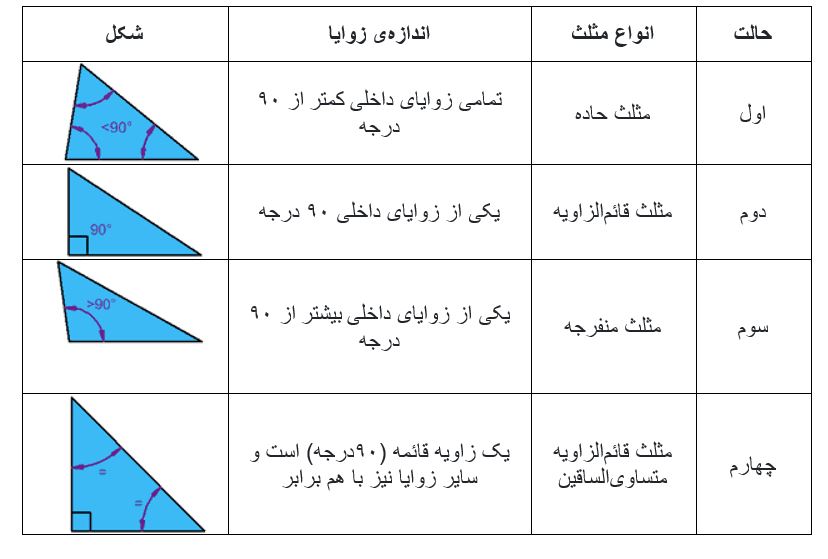
جدول 2

در صورتی که اندازه­ ی یکی از زوایای داخلی مثلث 90 درجه و مشابه حالت دوم و یا چهارم باشد (جهت مشاهده­ ی بهتر شکل و ارتباط بین معادلات، شکل 2 را ملاحظه فرمایید)، رابطه­ ی زیر بین اضلاع مثلث برقرار خواهد بود:

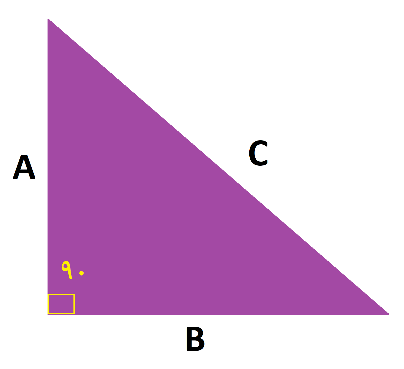
شکل 2. نمونه­ای از مثلث با زاویه­­ی داخلی 90 درجه

A² + B² = C²

در شکل 2، C یکی از اضلاع مثلث است که به عنوان وتر مثلث هم نامیده می­شود و برای محاسبه­ ی آن باید طبق رابطه­ ی بالا عمل شود تا اندازه­ ی ضلع C به دست آید. در بعضی مسائل ممکن است به جای اندازه­­ ی وتر، اندازه ی سایر اضلاع مثلث از شما خواسته شود. در پایان این مطلب، با استفاده از مثال ­هایی که ذکر می­شود با کاربرد این رابطه بیشتر آشنا خواهید شد، این رابطه همچنین به رابطه­ ی فیثاغورث هم معروف است.

اگر میخوای فقط چند ساعت تو روز و اونم بدون نیاز به حضور فیزیکی در جایی زمان بذاری و به صورت پاره وقت کاری انجام بدی که درآمد عالی داشته باشه، باید حتما صفحه آموزش تولید محتوا در سایت برترآموز رو ببینی!

محیط و مساحت مثلث

همانطور که گفته شد مثلث از اشکال هندسی پایه و پُرکاربرد در زمینه­ های مختلف است. از این رو در بسیاری از مسائل از جمله ساخت خانه، فضای سبز، کاشی­کاری، تزیینات داخلی و بسیاری از کارهای عمرانی و موارد دیگر از این قبیل، کاربرد و استفاده از این شکل هندسی دور از انتظار نخواهد بود. به همین علت ممکن است برای محاسبه­ ی بسیاری از مسائل ترکیبی و کاربردی در زمینه­ های مختلف، نیاز به محاسبه ­ی پارامترهایی از قبیل محیط و یا مساحت مثلث داشته باشید. به نظرتان با چه روشی می­توان این دو پارامتر را تعیین کرد؟ برای پاسخ به این سوال با ما همراه باشید

آموزش محیط مثلث

به شکل 1 با دقت بیشتری توجه کنید. محیط یعنی پیرامون، بنابراین برای محاسبه ­ی محیط مثلث تنها کافی است اندازه اضلاع آن را با هم جمع کنید. به­ طورکلی فرمول محیط مثلث طبق رابطه­ ی زیر می­باشد:

 محیط مثلث = مجموع اندازه اضلاع 

یا بر اساس نماد ریاضی و با توجه به شکل 1، محیط مثلث به صورت زیر نیز می­تواند نوشته شود:

محیط مثلث = AB + BC + AC 

آموزش مساحت مثلث

 

 

مثلث یکی از اساسی­ ترین شکل­ ها در هندسه است. ساده ­ترین و شناخته­ شده ­ترین فرمول را باید به خاطر بسپارید. برای تمام انواع مثلث‌ های ذکر شده در بالا، مساحت مثلث از یک فرمول محاسبه می­شود. اگر قصد محاسبه ­ی مساحت مثلث با سه ضلع را دارید، باید اندازه­ ی ضلع (قاعده) را ضربدر ارتفاع کنید و در نهایت جواب بدست آمده را تقسیم بر 2 کنید. پس فرمول مساحت مثلث برطبق رابطه­ ی زیر به دست می­ آید:

مساحت مثلث=     2÷   (قاعده­ ی مثلث × ارتفاع) 

جهت محاسبه­ ی مساحت مثلث همانطور که گفته شد باید قاعده یا همان اندازه­ی ضلع و ارتفاع را داشته باشید. اما اگر آن را نداشتید چه باید کرد؟ چگونه می­توانید مساحت مثلثی که فقط سه ضلع دارد را محاسبه کنید؟ اغلب اوقات پیدا کردن ارتفاع مثلث سخت است. در این موارد، بسته به اطلاعاتی که راجع به مثلث داده شده، می­توان از معادلاتی برای حل مسائل استفاده کرد. اگر هنوز مطمئن نیستید که چگونه مساحت یک مثلث را پیدا کنید، بهتر است با ادامه­ ی توضیحات همراه ما باشید.

در جدول 3، مطالب به صورت دسته بندی آورده شده است، تا با تطابق صورت مساله ­ی داده شده با موارد زیر، از یکی از فرمول ­ها برای حل مساله ­هایتان استفاده کنید.

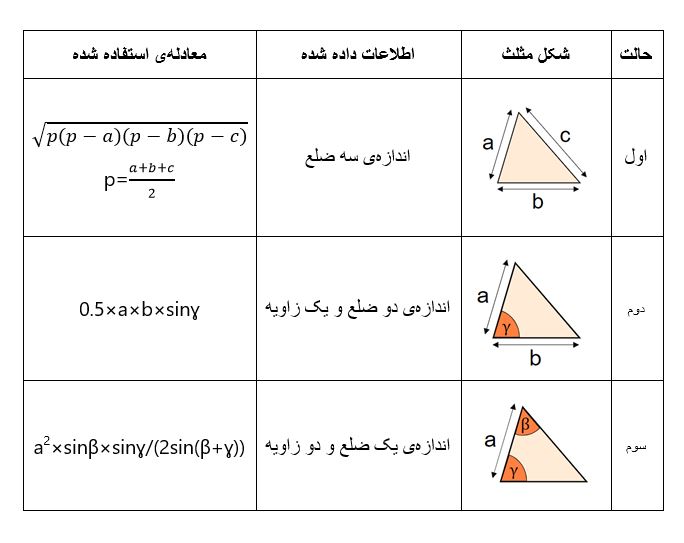
جدول 3

برای مثال در صورتی که در مساله ­ای اندازه ­ی یکی از اضلاع مثلث و اندازه­ ی دو مورد از زوایای داخلی مثلث به شما داده شود و از شما بخواهند مساحت مثلث را محاسبه کنید، باید از جدول 3 استفاده کنید و در ابتدا صورت مساله را با اَشکال داده شده مطابقت دهید. در این مثال، صورت مساله با حالت سوم در جدول مطابقت دارد، لذا باید از رابطه­ ی سوم در جدول برای حل مساله استفاده کنید.

در ادامه چندین نمونه از مثال­ های مختلف تعیین مساحت مثلث و کاربرد آن به روش­ های مختلف ارائه می­شود. اما بهتر است که در ابتدا با یک مثال ساده از تعیین محیط مثلث آغاز کنید و سپس با حل مسائل مربوط به اندازه ­گیری مساحت مثلث آشنا شوید.

مثال 1: در صورتی که اندازه­ی سه ضلع یک مثلثی 74، 92 و 102 سانتی­متر باشد، به نظر شما محیط آن مثلث چقدر خواهد بود؟

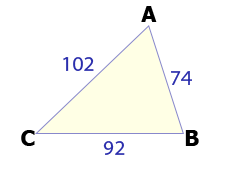
• پاسخ: همانطور که توضیح داده شد، محیط مثلث، یعنی پیرامون آن. پس باید برای به دست آوردن محیط مثلث، اندازه­ی تمام اضلاع آن را با هم جمع کنید. پس:

268 = 92 + 102 + 74 =محیط

 

مثال2: مساحت مثلث زیر چقدر است؟

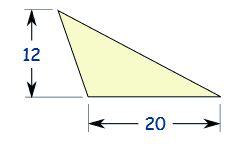
• پاسخ: همانطور که قبلا گفته شد، باید توجه داشته باشید که از هر ضلعی می‌توان به عنوان قاعده­ استفاده کرد، فقط باید مطمئن باشید که ارتفاع را از زاویه‌ای در نظر بگیرید که به قاعده عمود است. لذا عدد 12 ارتفاع مثلث است نه اندازه­ی ضلع. پس با استفاده از رابطه ی مساحت که در بالا ذکر شد، خواهیم داشت:

120 = 2 ÷  (12 × 20) =مساحت

 

مثال 3: مساحت مثلث  ABC را در صورتی که طول ضلع AB=38 mm و ارتفاع مثلث 42 mm باشد را محاسبه کنید.

• پاسخ: اندازه ­ی یک ضلع و ارتفاع مثلث داده شده است، با استفاده از فرمول محاسبه­ ی مساحت مثلث، می­توانید به راحتی مساله را حل کنید:

میلیمتر مربع 798 = 2 ÷  (38 × 42) =مساحت

مثال 4: ارتفاع مثلث متساوی ­الساقینی که طول یکی از اضلاع آن 37.8 میلی­متر و طول ضلع دیگر آن 23.1 میلی­متر است را طبق شکل زیر محاسبه و سپس مساحت آن را محاسبه کنید.

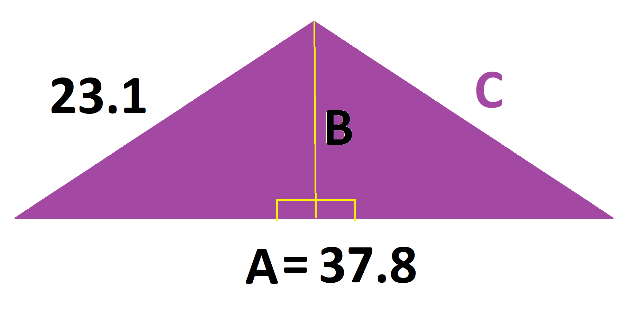
• پاسخ: برای حل این مساله، ابتدا باید ارتفاع مثلث (B) محاسبه شود. با توجه به شکل، مثلث متساوی­ الساقین از اتصال دو مثلث قایم ­الزاویه تشکیل گردیده است، لذا باید با استفاده از رابطه­ ی فیثاغورث که رابطه­ ی آن در بخش­ های قبلی نشان داده شد، مقدار B محاسبه شود. از طرفی با توجه به شکل، ابتدا باید اندازه­ ی طول ضلع A=37.8 تقسیم بر 2 شود تا مقدار اندازه­ ی ضلع برای هرکدام از مثلث ­های قایم­ الزاویه به دست آید. سپس در رابطه ­ی فیثاغورث قرار داده شود.

37.8÷2=18.5

تذکر: در رابطه ­ی زیر مقدار A همان 18.5 قرار داده می­شود. چون مقدار A مربوط به مثلث کلی است و در اینجا هدف تعیین ارتفاع مثلث بزرگ است که به عنوان یکی از اضلاع مثلث قایم­ الزاویه هم محسوب می­شود. لذا خواهیم داشت:

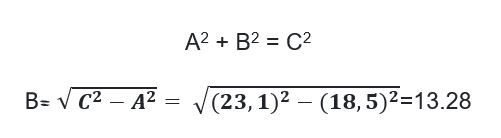
جهت محاسبه ­ی مساحت مثلث بزرگ خواهیم داشت:

24.15 = 2 ÷  (37.8 × 13.28) =مساحت

مثال 5: مساحت باغ مربعی، سه چهارم مساحت باغ مثلثی با اضلاع 80، 50 و 50 متر است. به نظر شما مساحت این باغ مربعی چقدر است؟

• پاسخ: برای حل این مساله ابتدا ساختار زمین مثلثی را مطابق شکل زیر درنظر بگیرید. سپس، با محاسبه­ی ارتفاع و مساحت مثلث طبق مثال قبلی، با توجه به اینکه در صورت مساله ذکر شده مساحت باغ مربعی سه چهارم مساحت باغ مثلثی است، می­توان مساحت زمین مربعی را نیز محاسبه نمود.

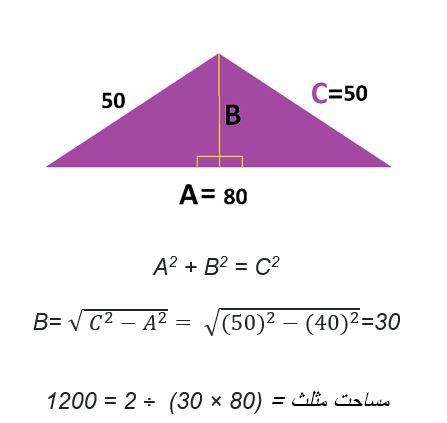
در نتیجه با توضیحات گفته شده، مساحت مربع برابر خواهد بود با:

مساحت مربع=  ×1200=900

مثال 6: در شکل زیر مساحت قسمت رنگی را محاسبه کنید:

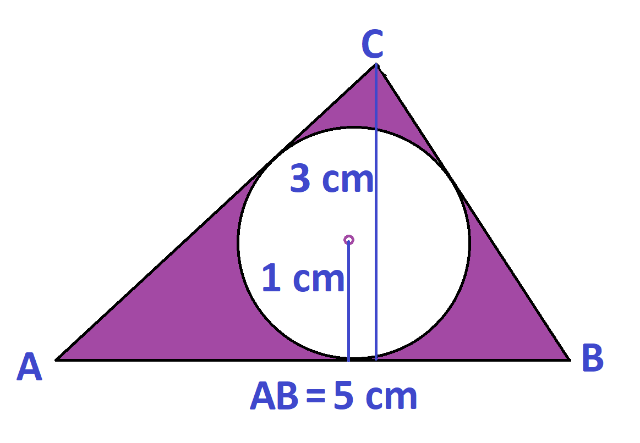
• پاسخ: برای حل این مساله بایستی آشنایی با مساحت دایره داشته باشید مساحت دایره از رابطه­ی (شعاع دایره×خودش×3.14 ) محاسبه می­شود. در اینجا شعاع دایره 1 cm است پس مساحت دایره خواهد بود:

3.14×1×1=3.14

برای محاسبه­ی قسمت رنگی، باید مساحت مثلث است را محاسبه نمود و سپس از قسمت رنگ­نشده (مساحت دایره) کم کنید تا مساحت قسمت رنگی محاسبه شود. در این مرحله، مساحت مثلث را با استفاده از توضیحات گفته شده، حساب کنید، پس خواهید داشت:

مساحت مثلث = 7.5 = 2 ÷ (3 × 5)

اکنون مساحت دایره را از مساحت قسمت مثلثی کم کنید تا مساحت قسمت رنگی به دست آید:

7.5-3.14=4.36

 

مثال 7: مساحت مثلث زیر را با اضلاع 3و4و6 محاسبه کنید.

• پاسخ: با توجه به اینکه اضلاع مثلث داده شده و مساحت آن مورد سوال می­باشد، برای حل این مساله به فرمولی که در جدول 3 ارائه شده است، مراجعه کنید. با استفاده از رابطه ­ی زیر و جایگذاری مقادیر داده شده، می­توانید مساحت مثلث را محاسبه کنید. به خاطر داشته باشید، مقدار p برابر نصف محیط مثلث است. یعنی:

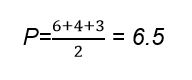
پس با جایگذاری در رابطه خواهیم داشت:

 

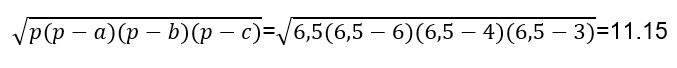
امید است مطالب ارائه­ شده در مورد مساحت مثلث، مورد توجه و استفاده­ ی کاربران محترم قرار گیرد.

در این قسمت می خواهیم بررسی کنیم که آیا رابطه ای میان مثلث و سایر اشکال هندسی وجود دارد یا خیر؟

در واقعیت امر این طور است که سایر اشکال هندسی مانند مربع ، مستطیل ، لوزی و متوازی اضلاع از کنار هم قرار گرفتن چند مثلث تشکیل شده است. برای مثال یک مستطیل را در نظر بگیرید که اگر قطر میانی آن را متصل کنیم شکل حاصل از دو مثلث تشکیل میشود و اگر دو قطر این مستطیل را وصل کنیم شکل حاصل از چهار مثلث تشکیل میشود پس مساحت یک چند ضلعی ماند مستطیل را از تشکیل 4 مثلث می توان به دست آورد.

مشابه همین مثال را میتوان با برای لوزی هم تشکیل داد که اگر دو قطر میانی را رسم کنید شکل حاصل تشکیل چهار مثلث را می دهد و از آنجایی که قطر های لوزی بر هم عمود هستند و تشکیل زاویه 90 درجه را می دهند، در نهایت چهار مثلث به وجود آمده قائم الزاویه خواهند بود که با مجموع 4 مساحت این مثلث قائم الزاویه میتوانید مساحت لوزی مذکور را به بدست آورید.

کاربرد مساحت مثلث در زندگی واقعی چیست؟

همانطور که در اطراف میبینم، در کنار زندگی روزمره ی ما تمامی اشیاء از یک شکل خاص هندسی پیروی میکنند و با یادگیری مساحت این موارد میتوانیم دانش خود را در این زمینه بالا ببریم و در هنگام وقوع موضوعی از دانش خود استفاده کنیم. برای مثال  ساختمان‌ها بر روی محدوده‌ هایی به شکل اشکال هندسی مانند مستطیل، مربع، مثلث و …. ساخته می‌‌ شوند. برای تعیین محدوده ساخت این ساختمان‌ها ، باید مساحت آن‌ها را تعیین کرد و باید نحوه به دست آوردن مساحت این موارد را هم از فبل آموخته باشید. در لوازم خانگی مانند میزها ، کشو ها و اقلام دکوری نیز می‌ توانند به اشکال هندسی مانند مثلث ساخته شوند. برای تعیین ابعاد روکش مورد نیاز برای پوشاندن سطح این لوازم، باید اندازه سطح مثلث تشکیل دهنده آن‌ها را از قبل آموخته و سپس محاسبه کرد.

حل چند مثال برای تفهیم بیشتر مطالب :

مثال : مساحت مثلثی با قاعده 6 سانتی‌ متر و ارتفاع 5 سانتی‌ متر چقدر است؟

حل : با بررسی صورت سوال متوجه میشویم که سرنخ های کلی یعنی قاعده و ارتفاع مثلث به ما داده شده است پس مانند زیر یک خلاصه نویسی در برگه خود انجام میدهیم.

h = ارتفاع = 5 سانتی‌ متر
b = قاعده = 6 سانتی‌ متر

فرمول مساحت مثلث‌ ها یه صورت زیر محاسبه میگردد:

A=(h×b)÷2

2÷ (ارتفاع×قاعده) = مساحت مثلث

2 ÷ (5×6) = مساحت مثلث

15 = مساحت مثلث

مساحت به دست آمده ، 15 سانتی‌متر مربع است. در مثال بالا، از هیچ شکلی برای نمایش مشخصات مثلث استفاده نکردیم. از این مثال می‌توان نتیجه گرفت که مساحت هر مثلثی با ارتفاع 5 سانتی‌متر و قاعده نظیر 6 سانتی‌متر، برابر با 15 سانتی‌ متر خواهد بود.

پیشنهاد میشود مقاله محیط مربع را مطالعه نمایید.

مساحت انواع مثلث ها

در قسمت های بالاتر با انواع مثلث ها آشنا شده اید حالا میخواهیم به بررسی مساحت انواع این مثلث ها بپردازیم: با ما همراه باشید.

مساحت مثلث قائم الزاویه :

مثلثی که یک زاویه 90 درجه در دل خود دارد، قائم الزاویه گفته میشود. که این زاویه قائم در مثلث توسط یک مربع کوچک □ روی زاویه 90 درجه ساق نمایش داده میشود. گاهی اوقات مثلثی را به شما میدهند با دو زاویه معلوم و زاویه سوم مجهول. در این حالت این وظیفه شماست که تشخیص دهید این مثلث چه نوعی است. همانطور که میدانید جمع زوایای داخلی مثلث 180 درجه است که شما در ابتدای مسئله باید اندازه زاویه سوم را تشخیص بدهید که اگر این اندازه 90 درجه باشد مثلث شما از نوع قائم الزاویه می باشد. در مثلث قائم الزاویه به ضلع روبروی زاویه 90 درجه وتر گفته می شود. نکته جالب در مورد مثلث‌ های قائم الزاویه این است که ساق‌ها، ارتفاع و قاعده نظیر یکدیگر به حساب می‌ آیند. برای همین دانستن مقدار آن‌ ها برای تعیین مساحت مثلث قائم الزاویه لازم است. طبق فرمول زیر داریم داریم:

2 ÷ (ساق دوم×ساق اول) = مساحت مثلث قائم الزاویه

مثال : مثلث قائم الزاویه ای را در نظر بگیرید که اندازه یک ساق آن 8 و دیگری 6 می باشد. مساحت مثلث مورد نظر را به دست آورید؟

حل : همانطور که در مثال گفت شد ، مثلث از نوع قائم الزوایه میباشد پس یک خلاصه نویسی به صورت زیر داریم.

ساق اول = 8

ساق دوم = 6

فرمول کلی                                    2 ÷ (ساق دوم×ساق اول) = مساحت مثلث قائم الزاویه

با جایگذاری در فرمول فوق داریم :

2 ÷ (6×8) = مساحت مثلث قائم الزاویه

سانتی متر  24 = مساحت مثلث قائم الزاویه

مساحت مثلث متساوی الساقین :

همانطور که در بالاتر ذکر شد، مثلث متساوی الساقین به مثلثی گفته می شود که دو ضلع هم اندازه و دو زاویه برابر دارد. سطح مثلث متساوی الساقین ، از ضرب قاعده در ارتفاع تقسیم بر دو به دست می‌ آید. در منابع آموزشی و درسی ، برابر بودن ضلع‌ های مثلث توسط خطوط کوچک عمود بر اضلاع (مانند |) نمایش داده می‌ شود. البته اگر دو زاویه مثلث با هم برابر باشند، اضلاع مقابل آن دو زاویه نیز با هم برابر خواهند بود حتی اگر علامت خطوط کوچک  در مثلث برای شما نمایش داده نشود. به ضلع‌ های برابر می گویند. در صورت قائمه بودن زاویه بین ساق‌ها ، یک مثلث قائم الزاویه متساوی الساقین تشکیل می‌ شود.

روش محاسبه مساحت مثلث‌های متساوی الساقین، تفاوتی با حالت کلی مساحت ندارد.

مساحث مثلث متساوی الاضلاع :

مثلث متساوی الاضلاع ، به مثلثی گفته میشود که سه ضلع برابر دارد. در منابع آموزشی و درسی ، متساوی الاضلاع بودن مثلث را ، با گذاشت علامت بر روی تمام ضلع‌ ها نشان می دهند. در صورت برابر بودن تمام اضلاع یک مثلث ، تمام زوایای داخلی آن نیز برابر خواهند بود. از این‌رو، اگر دو زاویه مثلث برابر با 60 درجه باشد ، آن مثلث متساوی الاضلاع است. مثلث متساوی الاضلاع ، یکی از انواع مثلث‌ های متساوی الساقین می باشد. با این تفاوت که در این مثلث‌ ها ، تمام اضلاع (قاعده‌ها)، تمام زوایا و تمام ارتفاع‌ها (به صورت جداگانه) با یکدیگر برابر هستند. این ویژگی ، یک روش به روش‌ های محاسبه سطح مثلث متساوی الاضلاع اضافه می‌ کند. به دلیل اضلاع برابر، فرمول محاسبه اندازه سطح مثلث‌‌‌های متساوی الاضلاع را می‌ توان به صورت زیر بازنویسی کرد:

A=√3/4a2 (مساحت مثلث)

فرمول مساحت مثلث به روش هرون

اگر اندازه سه ضلع مثلث را داشته باشیم میتوانیم از فرمول هرون برای محاسبه مساحت مثلث مورد نظر استفاده کنیم. قدمت این فرمول به حدود 2000 سال پیش باز می‌گردد.

فرمول مساحت مثلث به روش هرون به شیوه زیر محاسبه میشود .

A=√s(s−a)(s−b)(s−c)

A: مساحت
s: نصف محیط مثلث s=(a+b+c)/2
a: طول ضلع
b: طول ضلع
c: طول ضلع

فرمول مساحت مثلث رو چه جوری بدست بیاریم؟

خوب فرمول‌های اشکال هندسی معمولا جزو چالش‌های ریاضیات حساب میشه و دانش آموزان همیشه به این فکرند تا بتونند این فرمول‌ها رو به خاطر بسپارند. مهم‌ترین نکته در یادگیری فرمول‌ها این است که باید این موارد رو به صورت شهودی بارها مشاهده و با تمرین کافی بتونید این موارد رو یاد بگیرید.

فرمول مساحت مثلث اصلا پیچیدگی خاصی نداره . کافیه با تمرین و تکرار این فرمول را یاد بگیرید.

فرمول مساحت مثلث =   2÷   (قاعده‌ی مثلث × ارتفاع)

برای این که بتونید این فرمول رو به خوبی درک کنید باید با ارتفاع و قاعده‌ی مثلث آشنا باشید با مطالعه کتاب درسی مثال‌های زیادی در این زمینه وجود دارد.

آیا مساحت مثلث فرمول متفاوتی دارد؟ بررسی فرمول مساحت انواع مثلث‌ها

می‌دونیم که ما سه مدل مثلث ، متساوی الساقین ، متساوی الاضلاع و قائم الزاویه داریم. شاید الان فکر کنید که باید سه مدل متفاوت فرمول مساحت مثلث حفظ کنید ولی اصلا اینطور نیست با یادگیری چند روابط ساده می‌تونید تمامی این فرمول‌هارو یاد بگیرید! فقط کافیه انواع و تعریف‌های این 3 مثلث را بلد باشید.

فرمول مساحت مثلث قائم الزاویه ( همون مثلثی که یک زاویه 90 درجه دارد.) به صورت زیر است :

2 ÷ (ساق دوم×ساق اول) = مساحت مثلث قائم الزاویه فرمول

که در این جا ساق اول همان ارتفاع و ساق دوم قاعده مثلث است که متوجه شدیم فرمول اصلی تغییری نکرده و ما طبق همین فرمول پیش رفتیم.

فرمول مساحت مثلث متساوی الساقین ( همون مثلثی که دو ضلع هم اندازه و دو زاویه برابر دارد.) و متساوی الاضلاع ( همون مثلثی که سه ضلع برابر دارد.)  به صورت زیر است :

فرمول مساحت مثلث=     2÷   (قاعده‌ی مثلث × ارتفاع)

همانطور که می‌بینید اصلا با فرمول اصلی فرق نمیکنه ولی مهم اینه که شما بتونید ارتفاع و قاعده در مثلث رو به خوبی تشخیص بدید تا بتونید داخل فرمول مساحت مثلث جایگذاری کنید.