مساحت کره و نیم کره| به همراه فرمول و مثال

مساحت کره: روزانه با تعداد زیادی از اشیا کروی شکل برخورد میکنیم، این شکل بر خلاف اشکال دیگر که تا کنون در برتر آموز آن ها را مورد بررسی قرار داده ایم سه بعدی است و حجم دارد؛ همین مشخصه باعث میشود کره یکی از اشکالی باشد که در دنیای اطرافمان هر روز با آن برخورد کنیم. توپ ها، میوه هایی مثل پرتقال، گیلاس، سیب و…؛ همچنین کره یکی از اشکال هندسی است که به جهت گرد بودن و عدم زاویه‌ داری کمترین سطح مساحتی نسبت به اشکال دیگر را دارد، در نتیجه محاسبه مساحت کره و بررسی سطوح آن ساده بوده و همچنین با داشتن تنها یک پارامتر (شعاع) حجم و مساحت کره بدست می آید. امروز ما در این مقاله فرمول مساحت کره را بررسی میکنیم و حالات مختلف محاسبه ی مساحت کره را باهم یاد میگیریم؛ با ما همراه باشید. شما در پست های قبلی مساحت دایره، مساحت مثلث و مساحت مربع  و محیط دایره را یاد گرفتید.

کره چیست؟!

ارشمیدس اولین فرد در جهان بود که توانست مساحت برای کره را محاسبه نموده و فرمولی را برای محاسبات این شکل هندسی بیان نماید. بی‌شک با به دست آمدن مساحت کره می‌توان به‌راحتی ابزارآلات کارآمد کروی شکل در اندازه‌ها و سایزهای مختلف ساخت و با استفاده از فرمول مساحت کره می‌توان انواع سطوح اشکال هندسی را ارزیابی نمود.

اگر بخواهیم کره را تعریف کنیم میتوانیم بگوییم کره جسمی هندسی، کاملاً گرد و بدون زاویه در فضای سه‌ بعدی است و تمامی نقاطی که در سطح کره قرار دارند در فاصله یکسانی از مرکز کره قرار گرفته‌ اند؛ به این فاصله ثابت و یکسان شعاع کره گفته می‌ شود. انواع توپ‌ ها و گوی های فلزی و غیر فلزی و کره زمین ازجمله اشکال کروی هستند.

• در مورد تصویر: این یک طراحی از Olafur Eliasson میباشد که در سال 2019 در سانفرانسیسکو پیاده شده است، اساس این طراحی کره های فلزی ای هستند که یک سمتشان آیینه و نور های LED کار شده است، این کره ها طوری مقابل هم قرار گرفته اند که هنگامی که مقابل یکی از آن ها قرار میگیرید تونلی از تصویر خود و تصاویر غیر منتظره ای از محیط اطرافتان درونشان خواهید دید. آقای الیاسون این طراحی را seeing spheres  نام گذاری کرده است که به معنی دیدن کره ها میباشد!

ویژگی مساحت کره:

ویژگی‌های جالب کره موجب شده تا دارای کمترین سطح مساحتی نسبت به سایر اجسام و اشکال هندسی را دارا باشد. برخی از این ویژگی ها را در زیر میتوانید ببینید:

• تمامی نقاطی که در سطح کره قرار دارند در فاصله یکسانی از مرکز کره واقع‌ شده‌ اند. (شعاع)
• شعاع کره متقارن است و کره لبه و رأس ندارد.
• کره دارای کمترین سطح مساحت و بیشترین حجم داخلی نسبت به سایر اشکال هندسی است.
• قطر کره دو برابر اندازه شعاع است.

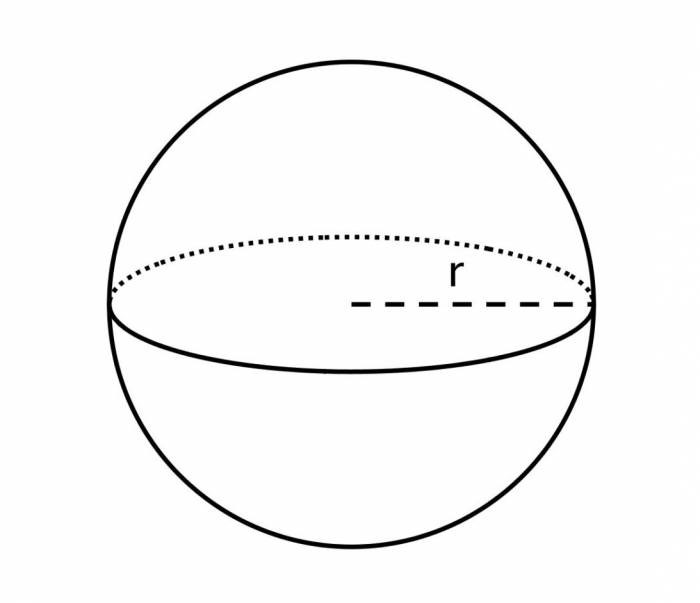
چگونه مساحت کره را محاسبه کنیم؟

فرض کنید شما دارای یک کارخانه تجهیزات ورزشی هستید و قرار است که توپ‌ های فوتبال جام جهانی 2022 را شما تولید کنید، فیفا برای تولید توپ‌ ها از شما خواسته سطح و رویه توپ‌ها را از یک ماده بسیار گران‌ قیمت پوشش دهید، برای اینکه بتوانید مقدار ماده اولیه مورد نیاز خود را ارزیابی کنید و بفهمید که چه مقدار ماده اولیه برای سطح کره نیاز دارید و بتوانید محصولات استانداردی ارائه دهید لازم است که در ابتدا مساحت کره را محاسبه کنید. برای این کار ابتدا باید شعاع کره (r) را به دست آورید چراکه گفتیم همه نقاط روی سطح کره تا مرکز آن دارای یک مقدار معین است و سپس از فرمول زیر استفاده نمایید:

مساحت کره = ۴ × عدد پی × شعاع × شعاع

و بیان این فرمول به زبان ریاضی عبارت‌ است از:

• مثال 1: برای مثال فیفا برای مسابقات توپ‌هایی با شعاع 5 سانتی متر در نظر گرفته که شما برای محاسبه مساحت کره در ابتدا 5 را در جایگاه (r) قرار داده و به توان می‌ رسانیم:

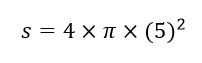
و با جایگزین نمودن عدد پی که مقدار ثابت 3.14 است (در مورد عدد پی در مقاله ی مساحت دایره بیشتر توضیح داده ایم) می‌توان مساحت کامل مساحت این کره را به دست آورد:

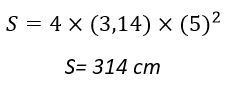
به عبارت بهتر می‌توان با استفاده از فرمول مساحت کره فهمید که توپ‌ های تولیدشده دارای چه مساحتی هستند؛ و چه مقدار الیاف برای پوشش سطح توپ‌ ها نیاز است. اگر فرمول مساحت کره با شکل را مورد بررسی و محاسبه قرار دهیم موجب درک هرچه بیشتر و عمیق‌تر مطلب می‌گردد.

• مثال 2: تولد دوست صمیمی‌ تان است و به دلیل اینکه او به جغرافیا علاقه بسیاری دارد به‌ عنوان هدیه یک مدل کره زمین برایش تدارک دیده‌ اید، حال برای کادوپیچ کردن هدیه نیازمند کاغذ کادو هستید برای محاسبه مقدار کاغذ مورد نیاز خود لازم است که مساحت کره را با استفاده از فرمول به دست بیاورید:

شعاع اگر 4 سانتی‌ متر باشد طبق فرمول مساحت کره:

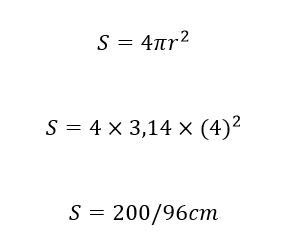
بنابراین شما برای کادوپیچ کردن این هدیه نیازمند 96/200 سانتی‌ متر کاغذ کادو هستید.

اثبات فرمول مساحت کره:

در هنگام مواجه با یک فرمول اولین موردی که به ذهن ما خطور می‌کند این است که این فرمول از کجا آمده و آیا واقعاً اطلاعات محاسباتی درستی در اختیار ما قرار می‌دهد یا نه؟ مساحت کره را نیز، هم می‌توان با استفاده از انتگرال و هم بدون استفاده از انتگرال به دست آورد.

• اثبات فرمول مساحت کره بدون انتگرال:

این روش اثبات فرمول مساحت کره بدون انتگرال بوده و بسیار ساده است:

برای مثال: یک کره را در یک استوانه محاط می‌کنیم و با این کار می‌توان ثابت کرد که از تصویر کره، سطح جانبی استوانه به دست می‌آید. مطابق شکل (3) با استفاده از تطابق بین استوانه و شکل کره به‌راحتی می‌توان فرمول مساحت کره با شکل را توصیف نمود.

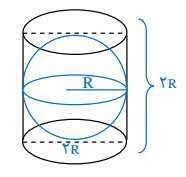
بنابراین می‌توان ثابت کرد که مساحت کره برابر است با مساحت جانبی استوانه؛ بر همین اساس مساحت جانبی استوانه که با حاصل‌ ضرب محیط استوانه (2*pi*r) در ارتفاع استوانه (2r) برابر است، را به دست می آوریم و آن را با Vc نشان میدهیم، درنتیجه داریم:

استوانه؛ بنابراین مساحت کره نیز برابر است S=4π

• اثبات فرمول مساحت کره از طریق انتگرال:

برای اینکه فرمول مساحت کره از طریق انتگرال ثبات نماییم در ساده‌ترین حالت می‌توان به طریق زیر عمل نمود:

ابتدا باید به این نکته پی ببریم که برای یک منحنی که با X(t) و y(T) پارامتری شده است، طول کمان برابر خواهد بود با:

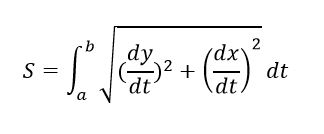
با جاگذاری فرمول مساحت کره و دوران منحنی حول محور x می‌توان به این صورت بیان داشت که:

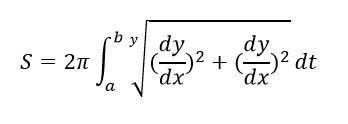
با چرخاندن نیم‌دایره حول محور می‌توانیم یک کره را ایجاد کنیم. معادلات این نیم‌دایره، 𝑋 =𝑟 cos⁡(𝑡)و 𝑦 =𝑟 برای  0≤𝑡 ≤𝜋است. بنابراین، خواهیم داشت:

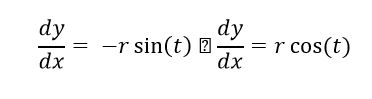
که با جاگذاری و بررسی متغیرها در فرمول نتیجه بدین‌ صورت خواهد:

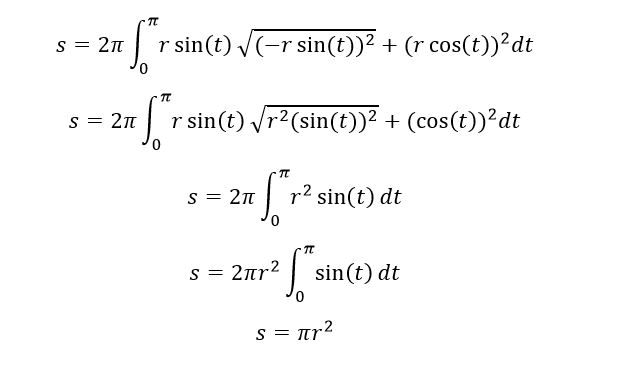
محاسبه مساحت نیم‌کره:

نیمکره همان نصف است به‌اضافه مساحت دایره‌ای که در کف آن قرار دارد تا  نیمکره پر شود.  لذا شما برای محاسبه مساحت نیمکره باید از فرمول زیر استفاده کنید:

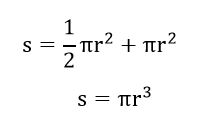
مثال: مساحت نیمکره پر به شعاع 3 را به دست  بیاورید. با جایگذاری 3 در مقدار r و عدد 3.14 در مقدار پی‌داریم.

در اینجا منظور از r همان شعاع کره یا نیمکره است و عدد پی همان 3.14 را بیان می‌کند. برای مثال کره‌ای با شعاع 3 است می‌توان مساحت نیمکره را این‌ چنین محاسبه کرد:

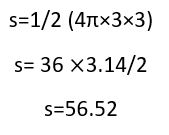
استفاده از انتگرال برای محاسبه مساحت کره:

براي محاسبه انتگرال روي يك سطح مهم‌ترین كاري كه ما انجام می‌دهیم، تصور كردن آن بر روي يك صفحه است و اين كار به اين دليل انجام می‌گیرد بتوان از طریق روش‌های انتگرال‌گیری بر روي سطوح دوبعدی مشخصات شکل و طرح سه‌بعدی را به زبان ساده‌تر دریافت نمود.

درواقع در این مبحث ما دیگر با فضای سه‌بعدی کار نمی‌کنیم پس توجهی به آن نخواهیم داشت بلکه، در اینجا با استفاده از دو نوع تابع، يعني توابع حقيقي (اسکار) و توابع برداري می‌توانیم مساحت را به دست آوریم.

تصوير زیر، يك كره را بر روي صفحه نشان داده كه بديهي است تصوير زیرین دایره‌ای به شعاع كره است:

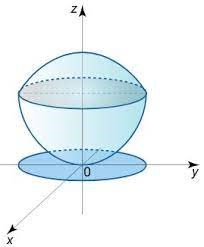
فرض كنيد رویه‌ ای مانند s به معادله‌ای g(x,y,z) = c و می‌خواهیم انتگرال تابع حقیقی (اسکار) مانند f(x,y,z) را روی s حساب کنیم، یعنی قرار است حاصل عبارت زیر را محاسبه نماییم:

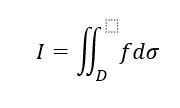
در این صورت اگر دایره D تصویر ناحیه s روی صفحه رویی مختصات قرار گیرد پس می‌توان تساوی زیر را بیان نمود :

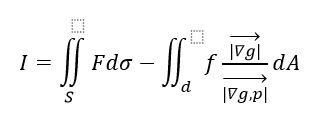
براي حل انتگرال سطح یعنی انتگرال تابع اسکار f بر روی سطح  s  باید مراحل زیر را انجام دهیم :

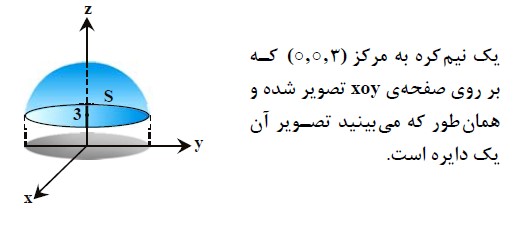
گام اول: ابتدا سطح را بر یکی از صفحات مختصات تصور می‌کنیم و ناحیه به‌دست‌آمده را D می‌نامیم.

گام دوم: با توجه به معادله g تلاش می‌کنیم را حساب کنیم:

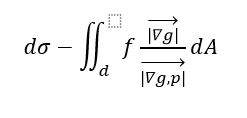
گام نهایی: در این مرحله d sigma به‌دست‌آمده را در انتگرال جای گذار کرده و بر ناحیه d انتگرال دوگانه عادی را حساب می‌کنیم .دقت کنید در این حالت اگر مثلاً صفحه تصویر ،صفحه xoy باشد، در انتگرال دوگانه ،فقط متغیرهای x,y داریم و لازم است در ضابطه‌ی f(x,y,z) به‌جای تمام z، مقدار آن را برحسب x و y وارد کنیم و با احتساب فرمول فوق می‌توان به‌راحتی از مساحت دایره‌های متصور شده مساحت کره را به دست آورد.

نتیجه‌گیری:

محیط زندگی ما پر از اشکال و ابعاد مختلف است که گاه برای بهره‌وری از یک محیط و یا ساخت یک وسیله با طرحی جدید را در پی دارد کره یکی از اشکالی است که در دنیای اطراف ما به چشم می‌خورد که مهم‌ترین آن زمینی است که ما در آن زندگی می‌کنیم، بنابراین استفاده از سطحی که موردنیاز ماست و می‌خواهیم بر روی آن‌یک عملیات عمرانی و… انجام دهیم نیازمند به دست آوردن اطلاعاتی نظیر مساحت سطح و حجم آن است، برای دست‌یابی به این اطلاعات دانش ریاضیات، فرمول‌ها و راه‌کارهایی ارائه نموده که ما بتوانیم دقیق‌تر و با کمتر خطا داده‌ها را ارزیابی نموده و آن را پردازش نماییم و بدین ترتیب برای انجام عملیات و فعالیت جدید کمترین ضریب خطا را داشته و بیشترین دقت پیش رو داشته باشیم لذا این موارد باعث می‌شود تا ما با نحوه محاسبه سطح انواع اشکال هندسی مخصوصاً کره آشنا شده و آن را بیاموزیم.